Circles ⇒⇒ Exercise 10.1

Question 1

How many tangents can a circle have ?

Solution :

The line that intersects the circle exactly at one single point are called tangent.

There are infinite number of points on circle , thus a circle can have infinitely many tangents.

Question 2 (i)

Fill in the blanks
(i) A tangent to a circle intersects it in____________ point (s)

Solution :

(i) one

The line that intersects the circle exactly at one single point are called tangent.

This means a tangent to a circle intersects it in only one point.

Question 2 (ii)

Fill in the blanks
(ii) A line intersecting a circle in two points is called a ____________.

Solution :

(ii) Secant

Question 2 (iii)

Fill in the blanks
(iii) A circle can have _____________ parallel tangents at the most .

Solution :

(iii) two

Only two tangents are possible AB and XY

Because a circle can have only one point just opposite to any other point.

Question 2 (iv)

Fill in the blanks
(iv) The common point of a tangent to a circle and the circle is called .

Solution :

(iv) Point of contact

Question 3

Fill in the blanks
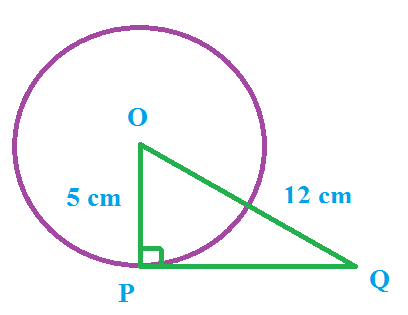
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ =12 cm, Length PQ is:

(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) √119 cm

Solution :

Given : OP = 5 cm. and OQ = 12 cm.

OP is the radius drawn from centre of the circle to tangent.

( Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

∴ OP ⊥ PQ

Since, OPQ is a right triangle, right angled at P.

In Δ OPQ

$$ Hypotenuse^2 = Base^2 + Perpendicular^2 $$

Using Pythagoras theorem,

$$ OQ^2 = OP^2 + PQ^2 $$

$$ ⇒ (12)^2 = (5)^2 + (PQ)^2 $$

$$ ⇒ (PQ)^2 = (12)^2 - (5)^2 $$

$$ ⇒ (PQ)^2 = 144 - 25 $$

$$ ⇒ (PQ)^2 = 119$$

$$ ⇒ PQ = \sqrt {119} $$

Therefore option D is correct,PQ = $ \sqrt {119} $

Question 4

Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.

Solution :

Draw a circle with any radius having centre O.

Draw a perpendicular OP on line MN (a line near to the circle) OP ⊥ MN , which intersects the circle exactly at point R.

Now, draw a perpendicular AB on point R of line OP (AB ⊥ OP). This AB is the tangent to the circle having centre 'O'

Now, take another point Z inside the circle on OP.

Draw a perpendicular XY on point Z (XY ⊥ OP).

And XY is the secant of the circle having center O and parallel to the line MN .

Here, AB is tangent to the circle having center O and parallel to line MN and line XY.